Multivariable Functions
Our world is a multidimensional world, so it is often necessary to work with functions of more than one variable. An example of a multivariable function is f(x,y,z) = 2xy + xz. It is easy to realize that length, width, and height might be represented by three variables.
When considering the rate of change of a multivariable function in one direction the method is to take a partial derivative. For those unfamiliar with partial derivatives, the method is to hold all variables, except the variable the partial derivative is being taken with respect to, as constants.
The symbol for a partial derivative of f(x,y,z) with respect to x is given by ∂f(x,y,z)/∂x. Using the above function as an example ∂f(x,y,z)/∂x = 2y + z, ∂f(x,y,z)/∂y = 2x, and ∂f(x,y,z)/∂z = x.

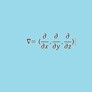







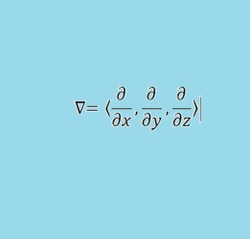

 UAPs, Formerly UFOs, If They Are Real How Can We Explain Their Arrival to Earth?on 12/18/2025
UAPs, Formerly UFOs, If They Are Real How Can We Explain Their Arrival to Earth?on 12/18/2025
 Polar Coordinate Systemon 12/16/2025
Polar Coordinate Systemon 12/16/2025
 Aurora Can Disrupt Electrical Devices And Even the Grid?on 12/15/2025
Aurora Can Disrupt Electrical Devices And Even the Grid?on 12/15/2025
 Overcoming Difficulties Encountered with Mathematicson 12/14/2025
Overcoming Difficulties Encountered with Mathematicson 12/14/2025



Comments
Since we are experiencing an occurrence that repeats, but was last observed before recorded history, and even humans, we can only conjecture from what we have determined. The periodic change was discovered by seafloor spreading as plates separate along plate boundaries. Knowing the rate of plate movement, and finding magnetic reversals in the rocks, the understanding of magnetic field reversal came about. Later, magnetic moment in volcanic rocks indicate that the last reversal happened quickly while lava cooled from an eruption. cURRENT COMPUTER PROGRAMS INDICATE THE FLIP IS NOT OVER THE ENTIRE PLANET ALL AT ONCE, AND WE ARE CURRENTLY EXPERIENCING LOCALIZED FLIPS. When will the main reversal happen id conjecture.
Thank you for your comment in answer to my previous observation and question.
Your answer advises us that magnetic-field reversal perhaps arises in "about 1000 years, but recent observations indicate maybe sooner."
Do we know about how much -- ;-[ -- sooner?
We do not know. The magnetic field reverses on about a 180000 year cycle, but it happens quickly. Rocks from a volcano showed the shift happens quickly. It does not happen over the Earth all at once. Since it has not happened in recorded history we do not know what to expect. Best guess it is should happen in about 1000 years, but recent observations indicate maybe sooner.
Thank you for your comment in answer to my previous observation and question.
Gravity changing by distance somehow caused me to consider magnetic fields changing over time.
Internet news describe the magnetic field developed over South America as displaying some weakening, in part of a regular strengthened, weakening, re-established magnetic field.
Might that mess the regular migrations of north- to south-flying, south- to north-flying birds?
Think about gravity. It points to the center of the Earth. The farther out something is the lesser force from the Earth's gravity is experienced. But at the same distance out the magnitude of the force is the same, regardless of location, only the distance is important.
The second subheading advises us that "In physics forces often change value depending on location, or how fast the magnitude of the is changing."
Which of location and magnitude is more influential?