Often Mathematics books are just a little vague as happens when something is so clear to the author that the author has no idea an explanation is needed. In other cases things are stated once, and if you do not pay attention to the details you can later find yourself asking how did we get to this point later. Trigonometry has several simple ideas that can be daunting if we just miss those few words, or made simple if we just understand a little deeper.
Another problem occurs in all of mathematics. Definitions are often wordy, and one might wonder why all the extra words that seem to be there just to clutter the idea being presented. Unfortunately, those words are usually needed, albeit for cases that might not occur at the level the material is intended.
The solution is a few clarifying words can be added to help make things understandable.








 The Linear Equation and Related Equations and Inequalitieson 08/15/2024
The Linear Equation and Related Equations and Inequalitieson 08/15/2024
 Understanding Calculus: A Simplified Approach to Derivativeson 08/05/2024
Understanding Calculus: A Simplified Approach to Derivativeson 08/05/2024
 Limits: Vital Building Blocks of Calculuson 08/01/2024
Limits: Vital Building Blocks of Calculuson 08/01/2024
 Mardi Gras Collectibleson 02/02/2023
Mardi Gras Collectibleson 02/02/2023


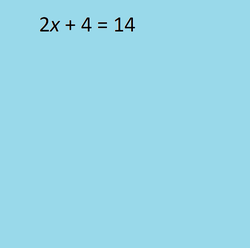
Comments
The "co" stands for complementary, meaning the angle that is added to obtain 90 degrees. All "co" functions look like the functions, but the values for 30 degrees for one are the values for 60 degrees for the other. In other words, tan(45 deg) = cot (40 deg), tan 30 deg) -= cot 60 deg), and so on. The same is true for sine and cosine, as well as secant and cosecant.
blackspanielgallery, Thank you for practical information, pretty pictures and product lines.
In particular I appreciate the examples that always anchor your explanations.
Are the attractive charts that you offer the only assists? Or, for example, would there be something similar for cotangents and tangents?