The linear equation is a cornerstone of algebra. Many other concepts can be reduced to linear equations, often by applying a few as one added idea.
The video that is shown below goes through a progression of complexity. I have examples that start with as few as one step. The progression takes the viewer into multiple step examples, and these include examples with symbols of grouping like parentheses and fraction bars.
It is obvious the symbols of grouping must be removed early in the solution process. To achieve this there is a need for the distributive process, a(b + c) = ab + ac.
Examples also include the special cases of those equations with no solution and those equations that have all real numbers as solutions.
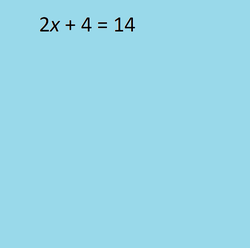
Understanding Calculus: A Simplified Approach to Derivativeson 08/05/2024
Limits: Vital Building Blocks of Calculuson 08/01/2024
Mardi Gras Collectibleson 02/02/2023
Choosing a Christmas Table Centerpieceon 11/14/2022
Comments
The early courses, college alg, trig, math for lib arts majors, ele ed math, finite math, discrete math, calculus, pre calc, first diff eq course, and linear algebra (Matrices) are freshman or sophomore courses.
Thank you for your comment below in answer to my previous observation and question.
The eighth comment box to your wizzley Limits mentions freshman and sophomore college math courses.
What might those courses be about? Would they start with algebra?
When I started teaching there were two remedial courses, intro algebra and intermediate algebra, which were later called foundation courses because remedial had a bad connotation. They were high school level for students too weak for college level math, and did not count for credit. Then came college algebra and trig or discreet math, depending on one's major, which served as math requirements for many. In my case those courses did not count. Both physics and math started with calculus, then differential equations. After that we picked from the more advanced courses. Engineering and chem were in our position, nothing less than calculus counted.
Thank you for your comment below in answer to my previous observation and question.
College algebra as a "low level" course intrigues me. It isn't what I expected even as I mulled the "lower" aspect of your answer "College algebra or lower."
What would be lower than college algebra!?
College algebra or lower.
Thank you for your comments below in answer to my previous observations and questions.
Your answer seven boxes down advises us that "The exponents of like bases determine an equation. Some few in low level courses might lead to other equations."
What are examples of "low level courses"?
Yes, and also no solution inequalities.
Thank you for your comment below in answer to my previous observation and question.
Does the definition below of special apply also to special-cased "equations that have all real numbers as solutions"?
Here it means something else, the condition, must be thought about. Rote, unthinking work does not work. Students can go through the method and not understand what has happened, especially not distinguish one case from the other.
Thank you for your comment below in answer to my previous observation and question.
The last sentence in your introduction advises us that "Examples also include the special cases of those equations with no solution and those equations that have all real numbers as solutions."
The description "special" associates in my mind with less common occurrences within a pool such as of linear equations.
Is that the case here, that solution-less equations involve a small part of linear-equation manifestations?