For linear inequalities we will start with the special cases first, since the special cases give great insight in the process.
First, inequalities of the form │ax + b│ < c where c is 0 or any negative number, or │ax + b│ ≤ d, where d is any negative number and d is any negative number, have no solution. An absolute value cannot ever be less than 0, so it cannot be less than a negative number.
Next, inequalities of the form │ax + b│ > d, or │ax + b│ ≥ d, where d is any negative number must always be true, so any value of x will solve the inequality. Hence, the solution set for this case is all real numbers.
The above cases utilize an insight into what an absolute value really is.
Now we consider the more general case. An absolute value being less than or being less than or equal to a non-negative number. We get sets of possible solutions, and we must consider only those solutions that make both parts of the set of possible solutions valid. Hence, we combine the two parts of the solution set with the word “and” which is the same as the intersection of the two sets or answers that we get when solving the inequalities. Any solution to only one of the two inequalities makes the absolute value inequality less than or at worse equal to a negative value, which is impossible.
As an example, find the solution set for │x + 5│ < 3.
(Many textbooks say to solve x + 5 < 3 and x + 5 > -3. This does not make clear why the < becomes >. Our approach makes this more understandable.
Inequality 1 is x + 5 < 3, with solutions x < -2 after subtracting 5 form each side of the inequality.
Inequality 2 is –(x + 5) < 3. Multiplying each side by -1gives x + 5 > -3. Notice when we multiplied by a negative number < became >. So, solving by subtracting 5 from each side of the inequality we get solutions x > -8.
Our solution set is -8 < x < -2. This is the same as x > -8 “and” x < -2.
Notice x can be negative. That is fine.
When the absolute value uses the > or ≥ symbol its two possible solution sets is combined using “or” and the solution set is any solution in ether possible solution set.
As another example consider │x - 9│ > 5. Our two inequalities are –(x – 9) > 5 and x – 9 > 5.
Inequality 1 is x – 9 > 5, which is solved by we add 9 to each side and get x > 14.
Inequality 2 is –(x – 9) > 5. First, multiply both sides by -1 to produce x – 9 < -5. Adding 9 to each side we get the solutions x < 4.
The solution set is x < 4 or x > 14.
Note: The absolute value must be isolated before starting. Had │x - 9│ - 5 > 0 been the problem │x - 9│ > 5 it would have had to be manipulated into the second form before starting.
If a problem starts with │x - 9│ < -3 simply indicate the problem has no solution.
If a problem starts with │x - 9│ > -3 simply indicate the problem has a solution set of all real numbers.
If a problem starts with │x - 9│ - 8 > -3 add 8 to each side, and solve │x - 9│ > 5 as was done above. Just seeing the negative number on the right side of the inequality is not enough to make a call of no solution or all real numbers are solutions, the absolute value must first be isolated on one side of the inequality.


















 The Linear Equation and Related Equations and Inequalitieson 08/15/2024
The Linear Equation and Related Equations and Inequalitieson 08/15/2024
 Understanding Calculus: A Simplified Approach to Derivativeson 08/05/2024
Understanding Calculus: A Simplified Approach to Derivativeson 08/05/2024
 Limits: Vital Building Blocks of Calculuson 08/01/2024
Limits: Vital Building Blocks of Calculuson 08/01/2024
 Mardi Gras Collectibleson 02/02/2023
Mardi Gras Collectibleson 02/02/2023

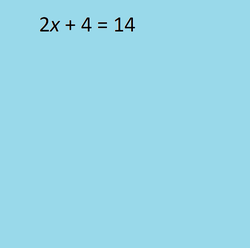

Comments
What happened is my Wizzley account does not pay off well enough. I figured out how to make a little more on Hubpages, and I also added videos on YouTube, which I can go back and embed in the articles. I check in on Wizzley to see if anything is new from some friends I have
made, I also write on contract when I can, which takes up time.
Your comment Feb. 8, 2021, in answer to my previous, same-day observation and question advised us that "I have six more that await the intro to be written, a minor thing. They will be coming out soon. And I also plan some physics."
In re-reading your wizzlies, might I be rewarded in their mustering more of the afore-mentioned retired professor simplifies series?
If students could get past the fear it might become easy.
Hi blackspanielgallery,
Your way of explaining things are self explanatory. I can see students gaining through your examples. Although I could score good marks in Maths, it was my brother who surpassed everyone.
I hope to go on to calculus, trig, and physics. Since these were ready I started here. I am hoping the Wizzley community accepts the type of article I propose, and other fields will soon be represented. I have single topics, since book length is too long for the platform, and people would need interactive ability to go to topice easily. Here, they can click on the other link, which I have been adding.
There is currently a demand for high school resources, 11-16, but advanced level maths and physics [16-18] will always find readers.
I have six more that await the intro to be written, a minor thing. They will be coming out soon. And I also plan some physics.
blackspanielgallery, Thank you for the practical information and the product line.
It's so enjoyable to go through the non-solution or solution of the equation step-by-step. Perhaps some of the fun results from the former, which I remember as quite delightful in algebra: an inherently unsolvable equation will not be the fault of the solver!
Will you write more on this retired professor simplifies series?