Any equation has two expressions that are equal. So, whatever is done to one side of the equation, if also done to the other, does not change the fact that the two expressions are equal.
The objective is to preform operations so as to cause the variable to be alone on one side of the equation, and not appear on the other side.
We will build complexity slowly. In the end you will have seen different examples that will help with your understanding.
Solve for x: x + 2 = 9
In order to get the variable alone on one side of the equation subtract 2 from each side.
x + 2 – 2 = 9 – 2, which gives x = 7.
Solve for x: 3x = 9
In order to get the variable alone on one side of the equation divide both sides by 3.
3x/3 = 9/3, which gives x = 3.
Solve for x: 2x + 1 = 4x - 7
Think that x stands for a number, so it can be treated as you would treat a number.
You must decide which way you want to send the variable, and send the number terms the other way.
2x – 2x + 1 + 7 = 4x – 2x – 7 + 7
8 = 2x
Now divide each side by 2.
8/2 = 2x/2, which gives 4 = x.
Note: It really does not matter which side of the equation the variable ends up on.
Solve for x: 2(x + 3) = -x – 9
Always remove the parentheses, or other symbol of grouping, first. This requires the distributive property, a(b + c) = ab + ac.
Eliminating the parentheses gives: 2x + 6 = -x – 9
Continue to solve. 2x + x + 6 + 9 = -x + x – 9 + 9
3x = 15
Divide by 3: 3x/3 = 15/3, which solves as x = 5.
Sometimes the variable disappears. If the result is a true statement all values for the variable are solutions, or all real numbers solve the equation. If the result is a false statement, the equation has no solution.
Solve for x: 2x + 5 = 3x + 5 – x
Collect like terms on each side of the equation.
2x + 5 = 2x + 5
Subtract 2x from each side of the equation.
2x – 2x + 5 = 2x – 2x + 5, or 5 = 5 (TRUE) So, all real numbers are solutions.
Solve for x: 2x + 5 = 3x + 6 – x
Collect like terms on each side of the equation.
2x + 5 = 2x + 6
Subtract 2x from each side of the equation.
2x – 2x + 5 = 2x – 2x + 6, or 5 = 6 (FALSE) So, the equation has no solution.
















 The Linear Equation and Related Equations and Inequalitieson 08/15/2024
The Linear Equation and Related Equations and Inequalitieson 08/15/2024
 Understanding Calculus: A Simplified Approach to Derivativeson 08/05/2024
Understanding Calculus: A Simplified Approach to Derivativeson 08/05/2024
 Limits: Vital Building Blocks of Calculuson 08/01/2024
Limits: Vital Building Blocks of Calculuson 08/01/2024
 Mardi Gras Collectibleson 02/02/2023
Mardi Gras Collectibleson 02/02/2023

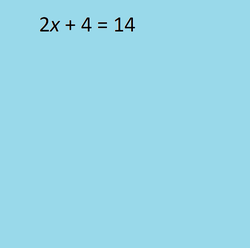

Comments
i probably will move on to trig or calculus in the future, but the pace will be slower. I had the algebra written for about a year, so it is easy to publish.
blackspanielgallery, Thank you for the practicalities and products.
Your explanations for making sense of variables and for tackling false and true statements leading to no solutions and solutions are most helpful. It must be such a relief for children and parents, math-anxious or not, to access user-friendly books on numbers, not just on beginning math but on to algebra...and perhaps geometry, trigonometry and calculus?