As physicists we take it as granted that the concepts in mathematics are just understood and accepted. We long ago learnt the proof and theory behind it, but have now just accepted that it is what it is, and why would anyone question it (mathematics is defined by human created axioms). The reality is that these abstract concepts are rarely taught, due to not being directly relevant to everyday life,

Negative, Imaginary, and Complex Numbers
by Audioworm
An introduction to some of the concepts of more advanced mathematics.
Limits of Natural Mathematics
Attempting to write an article on Relativity and Quantum Mechanics for layman is a challenge
Last night I was attempting to write an article on the new idea in physics of Geometric Unity. The theory is a combination of general relativity and quantum mechanics that hopes to form the framework of a General Universal Theory.
I was constantly running what I was saying by Jo to ensure that everything made sense to laymen. Throughout the conversation it became known to me that some ideas taken as obvious or inherent to those who spend most of their time dealing with advanced mathematics are often not even known to those who don't. A further problem arises from the natural numerical ability of individuals.
Mathematics is a human construct (though there is an argument over whether we discover or create maths), as a series of logical axioms that we define to mean certain things, and behave in certain ways. Maths is very different to science in its core as science is about fitting views to observations and data, while mathematics creates the rules to solve problems. Some of these definitions can appear quite circular, as the proofs that define them are often self-contained, but fully logical.
To get an idea about how we often have to create new sections of maths to solve what seem like very arbitrary problems, think of the question: What is 1 + 1? Instantly you will have probably said 2, but why? In an everyday circumstance we just accept that if you have one object, and bring in another of the same object, you now have two. But in maths this wasn't defined in a self-contained logical manner.
There exist a bunch of formal proofs to show this, the quickest one to read is here but the one I prefer is 362 page formal proof written by Betrand Russel and Alfred North Whitehead in Principia Mathematica. They developed a formal proof from the abstract formulation of set theory to eventually show that 1 + 1 = 2 is a fundamental argument.
Set theory was a way to explain what integers, and zero were, in a formal manner. The depth and brevity of the theory extends far beyond that, but a simple introduction can be shown here.
Within set theory we define all numbers as sets. Zero is given as the empty set, denoted as { }, Every number from here is defined as a set containing previous sets. One is the set that only contains the empty set, { { } }, and two is the set that contains both the empty set, and the set that only contains the empty, { { }, { { } } }. It gets increasingly lengthy as its purpose is not to be useful for everyday maths, but to set up logical formulation to something as simple as integers (whole numbers).
Negative Numbers
The first entry to really abstract maths
Hopefully you have made it through that rather lengthy introduction to some of the core ideas to the process of maths, and I haven't scared you off. From here onwards the article will be much more focused on the actual knowledge needed for a few of my upcoming articles. At times this may read as patronising, and at other times it may read as very heavy, but hopefully it can be followed through to the end.
Negative numbers are something most of us are familiar with, whether in the form of icy cold temperatures, or on the bank receipts telling you how much money you don't have. They are the absence of numbers. The first introduction is in the form of the number line, and as a result of subtraction.
![]() If you have nothing of something, and take three away you are three in debt of that object. It is the same if you have 5 of something and take 8 away, you are left with a debt of three. While debt is a way to initially rationalise negative numbers, it is important to forget it as we move on. Mathematics has negative numbers defined in specific ways, and trying to treat it as simply 'debt' will make what follows more confusing than it need be.
If you have nothing of something, and take three away you are three in debt of that object. It is the same if you have 5 of something and take 8 away, you are left with a debt of three. While debt is a way to initially rationalise negative numbers, it is important to forget it as we move on. Mathematics has negative numbers defined in specific ways, and trying to treat it as simply 'debt' will make what follows more confusing than it need be.
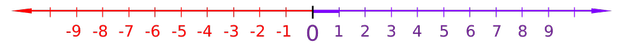 A number line showing negative numbers |
With this basic understanding of negative numbers further functions can be taken. Adding negative numbers is the same as subtraction, subtracting negative numbers in the same as positive numbers. This can be understood through the number line or debt analogy. Subtracting a negative number takes away the absence of the number, so results in the addition of the magnitude of the number.
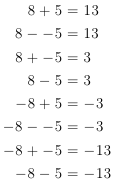 |
The magnitude of a number is its 'size' so the magnitude of both +7 and -7 is 7. Adding a negative is adding the absence of a number, so you are taking away the magnitude of the number.
Hopefully simple arithmetic with negative numbers is now within your reach, so we can move onto multiplication and division, and then on to some more interesting aspects of mathematics.
There are three simple rules for multiplying numbers that are signed (sign referring to either having a + or - in front of it, denoting whether it is positive of negative).
- Two positive numbers multiplied together gives a positive number
- A negative number multiplied by a positive number gives a negative number
- Two negative numbers multiplied together gives a positive number
There are some very formal proofs of this, but proof by example is easy to understand.
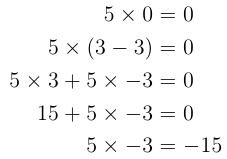 |
In the above equations we start with a simple initial point, a number times by zero is zero. We can however write 0 in different ways, a simple form being a number minus the negative of it (in our case 3). Without simplifying what is inside the brackets we can expand the brackets by multiplying each number in sequence by 5.
From this we get a an equation that equals zero, and we know what five times three is: 15. Now we know that fifteen plus five times negative three is zero. As we learnt above this means that five times negative three must be negative fifteen.
With this nice bit of deduction we can then do the same thing to show that two negative numbers multiplied together give a positive number.
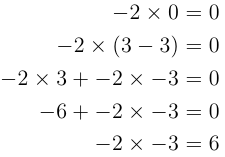 |
The same logic as used above applies to these equations. Hopefully all three rules are all understood.
The same depth of logic is not required to demonstrate the same is true of division. Division is the same mathematical process of multiplication, but multiplying by inverses instead. To divide by two, for example, is the same as multiplying by 0.5 (which is itself ½). The same is true for all forms of division, and therefore the same logic used above can equally applied giving three rules that are identical to the above
- Two positive numbers divided by each other gives a positive number
- A negative number divided by a positive numbers (or vice-versa) gives a negative number
- Two negative numbers divided by each other gives a positive number
Now negatives should feel more familiar and normal, and will help with the next two sections.
Imaginary Numbers
The square root of a negative number
In the above section we showed that when two positive or negative numbers are multiplied together we always get a positive number. This means that when any number is squared we always get a positive number.
To those not used to mathematical terminology squaring a number, denoted by n2 where n is any number, is multiplying a number by itself (52 is 5 x 5 which equals 25). The square root is the reverse of this process, finding which number when squared gives the starting number. So the square root of 1 is 1, of 4 is 2, of 9 is 3 (and so on). You can square root any number but only certain numbers produce whole number answers.
However, what if you wanted to find the square root of a negative number? It can't be done with natural numbers (all numbers we have covered up until this point) so we have to develop a new set of rules to deal with them. The solution mathematicians came up with is to create the imaginary unit i. i is defined as the square root of -1. There is no natural unit that when multiplied by itself gives -1, so there is no solution without the introduction of i.
From this we can can now calculate the square root of any negative number. So for the square root of -25 we get 5i (52 is 25, i2 is -1, and the two multiplied together give -25). There are much further uses of this new area of mathematics, and I will introduce them as becomes relevant, but for now we stick with just talking about complex numbers.
Complex Numbers
The combination of Natural and Imaginary numbers.
You've been introduced to imaginary numbers, and you are comfortable with natural numbers, so now you may be looking into how you can combine them.
Multiplying them together is nothing special, and simply behaves as you would expect. If you times 3 by 4i you get 12i, and if you were to divide 6i by 2 you get 3i. It gets a little more complex when you divide by something containing i.
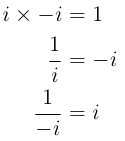 |
From the rearrangement on the left you can see what is done when you are dividing through by i. There is no magic trick to it, simply following the logic through blindly, and you can resolve all divisions by i to something that is simply in terms of i, without any divisions.
There are further functions you can do with i, but we are going to focus on complex numbers. A complex number is a number that is made up of both natural and imaginary numbers, in the form of an addition or subtraction. Simple in formulation but with some very neat properties.
A complex number takes the form a + bi where a and b are just numbers. The best way to visualise these is as vectors on what is known as the Argand plane. The Argand plane gives complex numbers as vectors on a Cartesian graph, with the vertical axis denoting the imaginary number line, and the horizontal axis as the real number line.
This view allows further manipulation of complex numbers. The first is addition and subtraction. Those knowledgeable of vectors will already know where this is going but for those that don't the process is relatively simple.
The first thing needed to know about vectors is that when adding or subtracting them you follow the top to tail method, in which you start the tail of the second vector at the top of the first one. It is the same for subtraction except that the second has all the value's signs flipped.
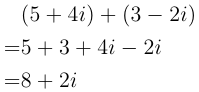 |
When multiplying complex numbers the rules of vectors are not used. With vectors multiplying them together takes two forms, either the dot product (which produces a number) or the cross product (which gives a vector). With complex numbers we treat it simply as a bracket expansion.
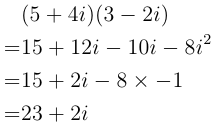 |
As can be seen as you expand the brackets you make sure each term from one of the brackets has multiplied the terms in the other brackets. You produce an i2 but as we know this is just -1 so you finish with just another complex number.
The multiplication, and general manipulation of complex numbers are extremely useful within quantum mechanics. Wave functions are often complex numbers, or contain exponents that include imaginary numbers.
Within quantum mechanics one of the features that is extremely important is the generation of probabilities from complex numbers. Quantum mechanics describes particles through a series of wave functions, which are descriptions of the probabilities of certain events. The probabilities are often given in the form of complex numbers, but we need them to be in the form of natural numbers.
To do this we have to find the magnitude of the complex number, which we do through a function called 'modulus squared'. Those who remember your school geometry lessons may remember the formulas for triangle, in particular the hypotenuse.
In right angled triangles (where one of the corners has an angle of 90o) the length of the longest side is given by a2 + b2 = c2 where a and b are the short sides (attached to the right angle) and c is the long side. We can see this in the image of the Argand plane above, but to produce this from straight written complex numbers and get the correct result every time we have to introduce a fudge factor.
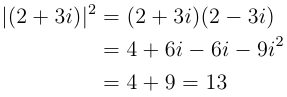 |
When finding the modulus squared of a complex number you multiply the complex number by its complex conjugate. The complex conjugate is the original complex number, but with the sign of the imaginary number flipped.
If this was not done then the result would still have i's in it, which is not useful for probabilities. It's also used to find the magnitude of the vector, as from geometry and our knowledge of the hypotenuse the results of the modulus squared are just the hypotenuse squared.
In Summary
The finale of this long and winding path
This article should hopefully have covered a lot of the preliminary material required to understand complex numbers, and to manipulate them in a basic form. Follow up articles on quantum mechanics, and eventually geometric unity will hopefully now be more comprehensible.
Physics without the maths is difficult to understand or appreciate, due to the limitations of our language. Standard spoken language is not able to deal with concepts that mathematics can formulate. When learning about new science I feel that you should not treat your audience like idiots, or assume they are incapable of understanding what is being written. Challenging people is important to their understanding as it allows them to think and work out what is going on for themselves.
If you have found any major issues with understanding written here I am happy to address it in further discussions
Thumbnail credits to =JakeLsewhere.
You might also like
Why do buses bunch?You wait half an hour for a bus and then three come along at once. But why?
Fractions—A Part of the WholeFractions are interesting numbers that indicate a part of the whole.










 How to Survive Going to University or Collegeon 08/02/2014
How to Survive Going to University or Collegeon 08/02/2014
 Ten TV Shows to Binge-Watch this Summer - Part 4on 07/16/2014
Ten TV Shows to Binge-Watch this Summer - Part 4on 07/16/2014
 Ten TV Shows to Binge-Watch this Summer - Part 3on 07/02/2014
Ten TV Shows to Binge-Watch this Summer - Part 3on 07/02/2014
 Ten TV Shows to Binge-Watch this Summer - Part 2on 06/18/2014
Ten TV Shows to Binge-Watch this Summer - Part 2on 06/18/2014


Comments
As a physicist and mathematician myself I have a problem with the word imaginary. It frightens students, and they think the imaginary numbers are not numbers of any sort. I prefer the two dimensional approach, and go into the absolute value using the Pythagorean Theorem as emphasis of what we are really dealing with. If only they had been called orthogonal numbers, or anything but imaginary. Nice work.
I was always fascinated by complex numbers and this served as a good refreshment.
I've got an article about Quantum Mechanics lined up, I was just waiting to finish this one so I had a good idea where to go into it.
I will cover it :P
Quite a good refresher on my calculus course(which i got an A in). I'm curious to know more about the quantum mechanics part you mentioned about "descriptions of the probabilities of certain events".
To me that is a resounding success :D
I actually did understand all of that! Ok, about halfway through I felt so far out of my depth that I couldn't even see the shoreline, but I persevered and it made sense. Good fight!