"Smeed's Law" is a rule pertaining to the relationship between road fatalities and traffic congestion measured by the proxy of the number of motor vehicles registered in a given population. How well does this somewhat fatalistic prediction, made in 1949, hold up against data collected in more recent years?
Smeed’s Law on Road Fatalities
by edstorm
Named after British statistician, RJ Smeed, Smeed’s Law is an empirical rule that relates traffic congestion to road deaths.
Named after British statistician, RJ Smeed, Smeed’s Law is an empirical rule that relates traffic congestion to road deaths, with congestion estimated based on the number of vehicles registered in a given country’s population. Simply, the prediction is that as the proportion of vehicle owners in a population increases, the number of traffic fatalities increases too.
Smeed’s Law is represented using the following formula, where D is the number of annual road deaths, n is the number of registered vehicles and p is population:
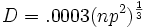
 |
Psychological Predictions
Although originally intended to apply to the roads of London, Smeed’s law was published in 20 countries, and by the time of his death in 1976, it had been applied in 46 countries, all showing results close to what his formula predicted.
Smeed hypothesized that group psychology plays a role in traffic fatalities. People take advantages of improved safety technology in both road infrastructures and in cars themselves to drive increasingly recklessly, causing the death count to rise. This behavior continues until total fatalities rise to a socially unacceptable level, at which point driver safety becomes more important, and people become less reckless. In other words, we drive recklessly until we’ve killed enough people on the roads that this becomes socially unacceptable. Smeed’s formula can be used in an attempt to define this number.
Another of Smeed’s predictions was that 9 miles per hour was the minimum speed at which drivers would continue to travel on London’s roads, and that if traffic congestion meant traffic flowed slower than that, they would avoid driving. Conversely, as speeds rise above this limit, the roads would attract more drivers until it became congested again.
 |
Modern Criticism
Critics now observe that road fatality rates are decreasing faster than the formula would suggest, as a result of improved safety measures, both in vehicles and in road infrastructure. A case in point is to be found in Brisbon, Australia. Traffic fatalities there fell from a peak of 1000 per year in 1970 to only 300 in 2009, despite strong population growth and an increase in the number of registered vehicles.
Smeed’s law may not be perfect, but his formula did hold up for 62 countries in a paper published in 1995, almost 50 years after his initial prediction. Some argue it’s still as useful as ever for predicting general trends, especially over longer periods of time.
Useful Links
Smeed's Law on Wikipedia
An overview of Smeed's Law on Wikipedia
Accident Data
A table showing numbers of road deaths related to traffic in a number of countries.
DSC Attorneys
Road accident attorneys in South Africa
You might also like
Emergency Winter Driving KitWhat do you need to keep in your car when driving in the winter? Here is a li...
Emergency Car Break Down Supplies For Winter TravelDo not get into your car this winter without these supplies.



 Herbal Medicine in South Africaon 08/20/2014
Herbal Medicine in South Africaon 08/20/2014
 Citroën, Europe’s First Mass Producer of Carson 07/04/2014
Citroën, Europe’s First Mass Producer of Carson 07/04/2014
 Use Smartphone Technology for Evidence Collectionon 07/03/2014
Use Smartphone Technology for Evidence Collectionon 07/03/2014
 Smart, Sneaky Solutions for Hiding Valuableson 06/13/2014
Smart, Sneaky Solutions for Hiding Valuableson 06/13/2014


Comments
Given that he said group psychology was the main driver of road behavior, I would think all teh constant road campaigns by governments are having an effect in re-educating people. Some young people have never ever drunk and driven, mainly because they've been taught from the outset not to - and that will have decreased road deaths too.