I’ve always had a fascination for pine cones, and later grew to have an equal fascination for their relationship to the Fibonacci sequence. It’s amazing how often this appears in nature, with some scientists saying that it can even be seen in hurricane formations and cancer cell replication. But it’s in the beauty of flowers such as daisies, sunflowers, even passion fruit where the Fibonacci sequence is at its most visible. Read on to find out more.

The Fibonacci Sequence
by Telesto
One of the most fascinating things about nature is the symmetry and beauty of so many plants. Does the Fibonacci sequence explain it?
Have you ever looked at a fir cone? I mean really looked? They are simple and beautiful and perfectly formed. I’ve loved them ever since I was a child rooting through the woods near to home.
When I studied botany, years later, I came to learn about the different types of fir cones, as well as flowers and plants and their different support systems and why one plant was like this when another was like that. But I didn’t learn about the magical sequences and symmetry so often seen in nature.
I don’t know exactly when I first learned about the Fibonacci sequence, but I do know that it was before Dan Brown wrote about it in The Da Vinci Code, although the reference to it there reminded me of how fascinated I’d been when I first learned about it.
So who was the famed Fibonacci, how did he become so knowledgeable about this and what exactly is a Fibonacci sequence?
Who was Fibonacci?
He was known by several different names – six in total, as far as I can tell. His full name was Leonardo Pisono Bigollo, but he was also known as Leonardo of Pisa, Leonardo di Pisano, Leonardo Bonacci, Leonardo Fibonacci and just plain Fibonacci.
Why so many names? He was born in around 1170, and his father was named Guglielmo Bonacci, which accounts for one of his Fibonacci’s names. Guglielmo was either a merchant, who travelled widely (probably the truth, since his son travelled widely and a poor shipping clerk is hardly likely to have been able to set him up for that) or he was a shipping clerk nicknamed Bonaccio, which meant “simpleton.” Fibonacci meant “son of a simpleton,” hence Fibonacci. (Two names done.)
Bigollo, in Tuscan dialect, means “well-travelled man,” which sorts out another of his surnames. Pisa? Well, in those days, Pisa was a republic, which honoured Fibonacci, so that accounts for another name.
Fibonacci may have been the son of a simpleton, but he certainly wasn’t stupid. He travelled around with his father and picked up a few things along the way, including the Hindu-Arabic numeral system.
We all know that the Romans were pretty smart and came up with of things that we still benefit from today, for example, they had under floor central heating long before we Brits had much in the way of elaborate homes to heat, but Roman numerals were pretty difficult for anything more than simple arithmetic – try doing long division with them and you’ll see exactly what I mean.
Fibonacci realised this and travelled throughout the lands surrounding the Mediterranean to study under the leading Arab mathematicians of the time. In 1202, he wrote a book called Liber Abaci – the Book of Calculation, and the thus the use of Hindu-Arabic numerals in Europe began.
What is a Fibonacci Sequence?
Liber Abaci is divided into three sections, the first of which relates mainly to the use of Arabic numbers, the second relating to problems relevant to merchants – the price of goods, how to calculate profit, how to convert the various currencies used in the Mediterranean countries, etc. The third section contains problems, one, of all things, relates to mating rabbits and it is this that led to the introduction of the Fibonacci sequence.
The question asked how many pairs of rabbits could be born to one mating pair in a year, if every month, each pair of rabbits gave birth to another pair every month. This was the result:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55 and so on. (Nowadays, we tend to start the sequence with a 0.)
Each number in the sequence is the sum of the preceding two numbers, so 89 would follow 55, etc.

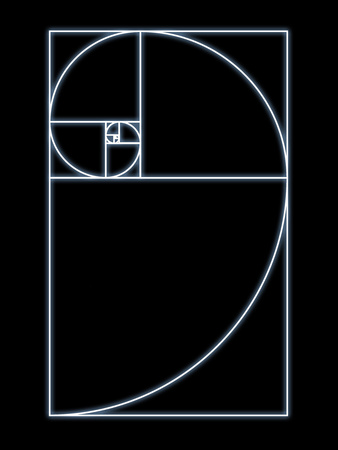
How does this show itself in Nature?
Living systems frequently grow in spirals – think of the double helix of DNA, or some of the tertiary and quaternary structures of protein molecules, and the seeds in the centre of a sunflower.
It transpires that these plant structures tend to follow a turning sequence of something like 0.618. Those who read the Da Vinci code will recognise this number too... The Golden Ratio, as it is called, is 1.61803.
In the Fibonacci sequence, if you divide any one of the numbers by the one before it, you get the golden ratio. (Yes, I did have to through a sequence of numbers when I was writing this to prove it to myself.)
In many plants, it appears that the sequencing just happens to be the most efficient way for the plant to be formed to perform whatever task is essential to the plant, such as the flowering of an artichoke, the fruit sprouts of a pineapple and my favourite, the pine cone, to name but a few. But it’s not just plants; it can also be seen in nautilus shells, and similar organisms. It can even be demonstrated at points in the human hand.
Is it just coincidence that so many living organisms follow this sequence? I don’t know, but it certainly is fascinating and the debate runs on and on.
You might also like
Lazarus Syndrome-- When the Dead Come Back to LifeAn unresponsive patient's heart begins to beat several hours after failed CPR...
Book Review: Hubble's Universe: Greatest Discoveries and Lates...Hubble's Universe by Terence Dickinson gives readers the most photogenic of 1...









 Identity Theft and How it Feelson 02/01/2015
Identity Theft and How it Feelson 02/01/2015
 Barts Hospital - a National Treasureon 01/24/2015
Barts Hospital - a National Treasureon 01/24/2015
 Urban Foxeson 01/11/2015
Urban Foxeson 01/11/2015
 How do you know which hosting platform to choose?on 01/03/2015
How do you know which hosting platform to choose?on 01/03/2015



Comments
Telesto, Thank you for the interesting article. Me too, I appreciate pine cones. Do you ever use them for their seeds or in teas?
Doesn't it seem incongruous that a civilization so known for building, road and ship construction -- which requires numbers-savvy engineers and mathematicians -- would have such cumbersome numerals of limited use? Do we know how the Romans achieved long division?