Wizzley

The Retired Professor Simplifies Algebra: Quadratic Equations

by blackspanielgallery

This simple understanding of algebra, the quadratic equation, is intended as a free resource for students and parents of students to help them grasp the ideas of algebra.

A quadratic equation is an equation that can be put in the form of a second degree polynomial equal to zero. A second-degree polynomial has an x2 term, and possibly an x term, and perhaps a constant term, but no other appearances of the variable. Sometimes terms have to be moved from the side of the equation that will become zero by addition or subtraction. Sometimes symbols of grouping will need to be removed, a process often requiring the distribution of multiplication over addition. The distribution property is a(b + c) = ab + ac. And sometimes like terms, those to with the variable raised to the same power, will need to be combined.

A quadratic equation can have as many as two solutions. Some have only one solution, which is repeated. It is possible the solutions are complex numbers. If they are, the solutions are conjugates of each other, meaning if one is of the form a + bi the other is of the form a – bi.

The Methods of Solving Quadratic Equations

We will examine three methods of solving quadratic equations, factoring, the completion of the square, and the quadratic formula.  Sometimes a technique like factoring, has limited use.  While the quadratic formula always works, it may not be the best choice, and does not make the underlying idea clear.  It is necessary to study all three methods in order to properly comprehend how we solve quadratic equations.

Needed Other Ideas

This algebra insight is intended to assist students and those helping students with the learning process. It is a free to use resource. This snipet covers factoring.
This is a free to use algebra resource. It is designed to make it easy to understand complex and imaginary numbers for students and those assisting students with learning.
Algebra simplified into a brief but thorough free resource can benefit both a parent helping a student and the student. This segment addresses linear equations.

Factoring

First, setting the quadratic equation equal to zero allows use of a powerful tool.  If two numbers are multiplied together, and that product is equal to zero, at least one of those numbers equals zero. 

 

If we think of factors as numbers, we can set each factor equal to zero, solve the two linear equations produced, and find the solutions of the quadratic equation.

 

Solve x2 + 6x = -8.

 

Add 8 to each side to get x2 + 6x + 8 = 0.

 

Next, factor to get (x + 4)(x + 2) = 0

 

Set each factor equal to zero, and solve the linear equations.

 

x + 4 = 0  x = -4

x + 2 = 0  x = -2

 

So, the solutions for the quadratic equation are -4 and -2.

 

Another technique one can use is completion of the square.  This is helpful in other problems, so develop the technique.

 

Since not every equation can be factored there is a need for techniques other than factoring to use in such cases.

 

In factoring we discover two special forms of perfect squares.

 

x2 + 2bx + b2 = (x + b)2

x2 - 2bx + b2 = (x - b)2

 

Our objective is to get one of these forms.

 

Solve x2 + 6x – 7 = 0

 

First, move the constant to the other side of the equation by adding the same value to both sides.  In this case adding 7 to each side is needed.

 

x2 + 6x = 7

 

Next, find b by dividing he coefficient of x by 2.

 

6/2 = 3

 

Now, square b and add b2 to each side of the equation.

 

x2 + 6x + 9 = 7 + 9

 

(x + 3)2 = 16

 

Now, take the square root of each side.  It is allowed.

 

x + 3 = 4 and x + 3 = -4

 

There are two roots that occur when taking the square root.

 

Next, add -3 to each side of each equation.

 

x = 1 and x = -7

 

So, 1 and -7 are the solutions of the quadratic equation.

Quadratic Formula

The quadratic formula is found by solving by the completion of the square for a general equation and inserting the values when the formula is used.

 

Solve ax2 + bx + c = 0

 

Add -c to each side.

 

ax2 + bx = -c

 

Next, divide by a.

 

x2 + bx/a = -c/a

 

Take half of the coefficient of x and divide by 2.

 

b/2a

 

 

Square the result.

 

b2/(4a)

 

This is what is needed to be added to each side of the equation.

 

x2 + bx/a + b2/(4a2) = b2/(4a2) – c/a

 

 

Make the right side of the equation a single fraction with the common denominator of 4a2.

 

x2 + bx/a + b2/(4a2) = (b2 –4ac)/(4a2)

 

 

The left side of the equation is a perfect square.

 

(x + b/2a)2 = (b2 –4ac)/(4a2)

 

Take the square root of each side.

(x + b/2a) = ±(b2 –4ac)1/2/(2a)

 

So, x = (-b ±(b2 –4ac)1/2)/(2a)

 

So, to solve a quadratic equation we get zero on one side, then use the quadratic formula. 

 

Solve x2 + 6x = 7 using the quadratic formula.

 

Subtract 7 from each side of the equation. 

x2 + 6x – 7 = 0

 

Identify a, b, and c:  a = 1, b = 6, and c = -7.

 

x = (-6 ± (62 – 4(1)(-7)1/2)/(2x1)

 

x = (-6 ± 641/2)/2

 

x = 1 and x = -7 are the solutions.

 

It is important to know that when the value under the radical symbol is positive there are two real solutions, when it is zero there is one real repeated solution, and when it is negative there are two complex number solutions that are conjugates of each other.

 

The quadratic formula is nothing more than completing the square for a general equation.  Once it is done, it can just be used thereafter.  Or, you can just accept it and plug in. 

This article contains links to affiliate programs and Adsense advertising.  These must use cookies to allow for proper crediting, and allow me to earn from qualifying purchases. As an Amazon Associate I earn from qualifying purchases.

Updated: 02/10/2021, blackspanielgallery
 
Thank you! Would you like to post a comment now?
1

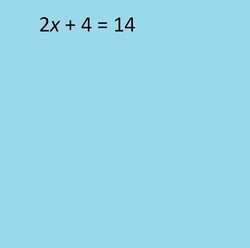
Comments

Only logged-in users are allowed to comment. Login
blackspanielgallery on 02/12/2021

I prefer the use of matrices and the row reduction echilon technique, too advanced for the article but nice with a good graphing calculator. Completing the square gives the quadratic formula, and is the theory behind it, but completing the square also is used to find the center of a circle, or work with other conic sections of the the elllipse, hyperbola, and parabola, so we cannot ignore it, This is a difficulty in teaching, we know what is coming, but the student does not, so the student will often say I can ignore a concept and still solve every problem. A few weeks later it occurs to the student there was a reason the material was there.

DerdriuMarriner on 02/12/2021

blackspanielgallery, Thank you for the practicalities and products.
Which of the three methods do you prefer? Where does completing the square fit between the limited use of factoring (my favorite because the most fun, albeit not always the most applicable) and the workability of the quadratic formula despite the latter's not always making "the underlying idea clear"?

You might also like

The Linear Equation and Related Equations and Inequalities

This is a good place to start algebra, and give enough examples why the basic...

The Retired Professor Simplifies Algebra: Linear Inequalities

This is the second part of a free resource to help with the basic understqand...

Disclosure: This page generates income for authors based on affiliate relationships with our partners, including Amazon, Google and others.
Loading ...
Error!