Wizzley

The Retired Professor Simplifies Algebra: Systems of Equations

by blackspanielgallery

Insights into algebra with attention to systems of linear equations is the focus here. This free to use simple explanation of a complex topic is intended for students and parents.

Occasionally, we need to find a point where two linear equations are both satisfied.

There are several approaches one can take. Which one you select may depend on how much easier finding a solution with that method is over other methods.

While any of the techniques is allowed for any problem, it is wise to reduce the amount of work. Selecting the most cumbersome technique can allow more careless errors to occur. Which technique is the more cumbersome is often a matter of the numbers in a particular problem.

Another reason for learning all of the techniques is to develop the skills necessary for solving nonlinear equations. This happens in College Algebra. In nonlinear system of equation problems often there is a technique that works that must be selected. So, always prepare for what is coming.

The Substitution Methor

The substitution method involves solving one equation for either variable, then replacing that variable in the other equation by the expression found for that variable.

 

Solve the system 3x + 2y = 7 and 6x + y = 8.

 

It is easy to solve the second equation for y since the coefficient of y is 1.

 

Add -6x to each side of the equation.

 

6x + (-6x) + y = -6x + 8

 

y = -6x + 8.

 

Now substitute for y in the other equation. 

 

3x + 2(-6x + 8) = 7

 

3x – 12x + 16 = 7

 

-9x + 16 = 7

 

-9x + 16 – 16 = 7 -16

 

-9x = -9

 

x = 1

 

Substitute into either equation and solve for the other variable.  (Note, it can be after the equation has been solved for that variable.)

 

y = -6x + 8

 

y = -6(1) + 8 = 2

 

The solution is (x, y) = (1, 2).

Special Cases

As with linear equations, if the variables all disappear the system of equations have no solution when a false statement results, and an infinite number of points solve the system of equations when a true statement results.

 

Solve the system of equations x + 2y = 4 and -6x – 12y = -24.

 

Solving x + 2y = 4 for x gives x = -2y + 4.

 

Substituting in the other equation gives

 

-6(-2y + 4) – 12y = -24

12y – 24 – 12y = -24

 

-24 = -24

 

This is a true statement, so we have an infinite number of points that solve the system of equations.

 

The relationship between the variables is needed, since many other points are not solutions. 

 

Pick one variable and assign it t, where t is any real number.  In this problem, since we know y in terms of x, make x = t.

 

y = -6x + 8 gives y = -6t + 8

 

(t, -6t + 8), where t is any real number, describe the infinite number of points that solve the system of equations.

 

Solve the system of equations x + 2y = 5 and -6x – 12y = -24.

 

Solving x + 2y = 5 for x gives x = -2y + 5.

 

Substituting in the other equation gives

 

-6(-2y + 5) – 12y = -24

12y – 30 – 12y = -24

 

-30 = -24

 

This is a false statement, so the system of equations has no solution.

Elimination or Addition Technique

It is allowed to multiply both sides of an equation by the same number, except do not use zero because it erases the information in the equation.

 

In order to eliminate a variable, multiply one, or both, equations so a variable is eliminated when the two equations are added together.

 

Solve 3x + 2y = 7 and 2x + 4y = 10

3x + 2y =   7  Multiply by -2 to eliminate y.

2x + 4y = 10

 

-6x – 4y = -14

  2x + 4y =  10

-4x          =   -4

 

So, x = 1

 

Substitute into either equation and solve for y.

 

3(1) + 2y = 7

2y = 7 – 3

2y = 4

y = 2

The solution is (1, 2)

 

The same rules apply for the no solution or infinite number of solutions cases.  If both variables disappear, ask if the result is true (infinite number of solutions) or false (no solution).

 

For three equations pick equations two at a time and eliminate a variable.  Next, do the same for two equations, one of which is the equation not yet used.  Eliminate the same variable.  You get a system with two equations and two remaining variables.  Solve as above.  Next, substitute back into one of the original equations and solve for the third variable.

Other Topics

Algebra simplified into a brief but thorough free resource can benefit both a parent helping a student and the student. This segment addresses linear equations.
This is a free resource on understanding algebra, and presented in a short presentation aimed at making things clear. It may help thoses studying algebra and those trying to help.

This article contains links to affiliate programs and Adsense advertising.  These must use cookies to allow for proper crediting, and allow me to earn from qualifying purchases. As an Amazon Associate I earn from qualifying purchases.

Updated: 02/11/2021, blackspanielgallery
 
Thank you! Would you like to post a comment now?
2

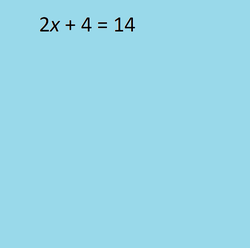
Comments

Only logged-in users are allowed to comment. Login
blackspanielgallery on 05/03/2021

Right now students need as much help as is available.

WriterArtist on 05/03/2021

Examples reduce the complications. You have taken good initiative to explain systems of equations. If you take online courses, probably the students can benefit more from the interactive sessions.

blackspanielgallery on 02/12/2021

I would think it should be part of any algebra course, so whatever level one is at should include systems of equations.

DerdriuMarriner on 02/12/2021

blackspanielgallery, Thank you for the practical information and the product line.
What is the earliest level at which equation systems are introduced?

You might also like

The Linear Equation and Related Equations and Inequalities

This is a good place to start algebra, and give enough examples why the basic...

The Retired Professor Simplifies Algebra: Linear Inequalities

This is the second part of a free resource to help with the basic understqand...

Disclosure: This page generates income for authors based on affiliate relationships with our partners, including Amazon, Google and others.
Loading ...
Error!