First, we answer the question, “What is factoring used for?”
Students need to be given a reason for studying. The answer here is this is a powerful tool that can be used in equation solving.
In factoring we break down expressions to two or more expressions that are multiplied by each other. The parts used in that multiplication are called factors.
First, remove any common factor.
Factor 5x3 + 5x2 + 25x. each term contains 5x, so it can be removed as a common factor.
5x(x2 + x + 5)
It is important that common factors be removed first, since doing this makes the problem easier.
Factoring by grouping is a form of removing common factors.
Factor x3 – x2 + 7x – 7
Group the first two terms, and also group the second two terms. Take out any common factor from the group.
x2(x – 1) + 7(x – 1)
Notice x – 1 is a common factor.
(x – 1)(x2 + 7)
It should be pointed out that two groupings will work, but the third does not. So, if pairing terms one way does not work it may be that pairing terms in a different way will be worth doing. In an advanced approach terms can be grouped three or more at a time into a single group.
Factoring a trinomial is not always possible, but the technique to factor trinomials is well worth learning.
Factor x2 - 3x – 4
Note that the negative signs are parts of the numbers. Algebra is built on two operations, addition and multiplication, and subtraction is thought of as adding a negative number. Likewise, division is thought of as multiplying by a reciprocal.
We want two numbers that add to -3, and multiply as -4.
(x + a)(x + b) = x2 + ax + bx + ab = x2 + (a + b)x + ab
So, we need two numbers that multiply together to give, in this case, -4 and 1. The possible number pairs are (-1, 4), (-2, 2), and (-4, 1). In order to get the middle term to be -3x, we need that pair of numbers from the list that add to -3. That is -4 and 1.
x2 - 3x – 4 factors as (x – 4)(x + 1).
When x2 has a coefficient it also must also be factored. However, changing all of the signs gives nothing new, so it need not be done for the lead term.
Factor 2x2 – 5x + 3.
The possible pair for the 2 is (2, 1). (Notice -2, -1 will lead to repetitions.) The possible pairs for the 3 are (-1, -3) and (1, 3). Now we must be careful where we place things. The -5 must come from multiplying factors of the 2 by factors of the 3. 2(-1) and 1(-3) add together to get
-2 + (-3) = -5.
Remember, we are undoing polynomial multiplication.
(2x - 3)(x - 1) has the 2(-1) and the 1(-3). Proper placement is critical.
The Linear Equation and Related Equations and Inequalitieson 08/15/2024
Understanding Calculus: A Simplified Approach to Derivativeson 08/05/2024
Limits: Vital Building Blocks of Calculuson 08/01/2024
Mardi Gras Collectibleson 02/02/2023
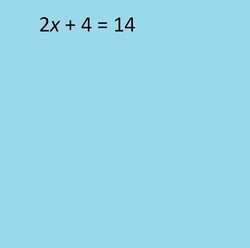
Comments
Likewise, but only the administrators can help with that.
Educators should commit themselves to life long learning, but not all do. I have encountered one or two whom I would call ignorant.
Unfortunately, in this state it is more so than in most. Tense id not important to many of them. And care for the math is also often lacking. Our universities have a wide range from academic excellence to what I would call diploma mills. I taught where we hired some weak people from one certain university, and it was obvious.
I was for a short time copy editor of a school newspaper and my experience confirms that not every teacher has writing skills.
Each state handles education differently, and some introduce advanced topics earlier than others. I once reviewed textbooks intended for use in various states, and all is not equal. In fact, the teachers who contributed to those books had different skill levels, some had difficulty keeping a paragraph in present, past, or future tense, and jumped from one to another. Others had teachers who could actually write English.
blackspanielgallery, Thank you for the practical information and the product line.
How early is factoring being introduced in schools? Master gardeners and master naturalists here may fulfill their yearly Cooperative Extension hours through helping to teach fourth-grade science. Fourth-grade science seems like middle school although the students handle the leap well since the commonwealth school system prioritizes quality teachees and teachers.