Wizzley

The Retired Professor Simplifies Algebra: Radical Equations

by blackspanielgallery

This is a simplified look at algebra, redical equations, which are equations with square roots, cube roots, and so on. It is intended to give insights to students and turors.

A radical equation is one with a square root, cubic root, or any other root.

The method is to isolate the radical on one side of the equation, and raise the expression to the appropriate power so as to remove the radical. A square root is raised to the second power, and so on. Remember, whatever you do to one side of an equation must be done to both sides of the equation.

If there are more than one radical, the process is repeated until all radicals are removed.

Once the radicals are removed, solve the linear or quadratic equation as you normally would.

One added step is needed at the end. Check the answers if the two sides of the equation were raised to an even power. The problem here is that solutions to a squared equation, or any other even power, may or may not solve the original equation.

To illustrate the problem, start with an easy equation, x = 1. We know the solution is 1. Now square each side of the equation. x2 = 1 has two solutions, x = -1 and x = 1. Only one of the solutions works in the original equation.

The problem occurs when raising each side of an equation to an even power. Odd powers do not cause extraneous solutions.

[Note: Because square root symbols added by the equation editor do not appear on this platform I am going to use the 1/2-power as an alternative.]

Do not read between the lines. In some cases, neither solution of the new equation solve the original equation, and in others both solutions work.

Illustrating the Method

Solve the equation (x + 2)1/2 + 1 = x + 3.

 

First, subtract 1 from each side to isolate the radical.

 

 (x + 2)1/2 = x + 3 – 1

 

(x + 2)1/2 = x + 2

 

Next, square each side of the equation.

 

x + 2 = x2 + 2x + 2x + 4

 

Be certain you have properly multiplied the polynomial.

 

x + 2 = x2 + 4x + 4

 

This is a quadratic equation, so subtract x + 2 from each side.

 

0 = x2 + 3x + 2

 

This can be factored, or you can use the quadratic formula. 

 

0 = (x + 2)(x + 1)

 

Solve x + 2 = 0 to get x = -2, and x + 1 = 0 to get x = -1.

 

Check by plugging into the original equation.

 

Both solutions work.  So, 1 and 2 are the solutions to the original equation.

 

Special Case

One special case might come up, a square root equal to a negative number.  Such equations have no solution.

 

As an example, try to solve (x + 5)1/2 + 7 = 4.

 

Subtract 7 from each side to get (x + 5)1/2 = -3

 

Since the square root cannot equal a negative number in the real number system there is no solution.

 

The same cannot be said if a variable appears on the side of the equation opposite the radical.  Only after a possible solution is obtained and inserted for the variable can a determination of the sign of an expression be made.

 

This article contains links to affiliate programs and Adsense advertising.  These must use cookies to allow for proper crediting, and allow me to earn from qualifying purchases. As an Amazon Associate I earn from qualifying purchases.

Updated: 02/11/2021, blackspanielgallery
 
Thank you! Would you like to post a comment now?
2

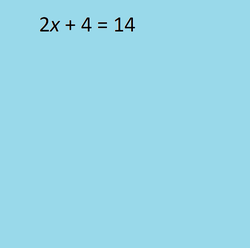
Comments

Only logged-in users are allowed to comment. Login
blackspanielgallery on 02/12/2021

No, the squared equation often has two solutions, but both might solve the original equation, one might and none might. However, there could be more than two,or perhaps only one. In solving the linear equation and the quadratic equation, either of which could occur, there is a set of rules to follow, and if the variable disappears an infinite number of solutions is possible.

DerdriuMarriner on 02/12/2021

blackspanielgallery, Thank you for the practical information and for the product line.
Is there a rule for when even power solves equations and when not?

You might also like

Learn Algebra and Trigonometry with Rap Videos

Learn the hard to grasp Algebra and Trigonometry basics from inspiring math t...

The Retired Professor Simplifies Algebra: Factoring

This algebra insight is intended to assist students and those helping student...

The Retired Professor Simplifies Algebra: Linear Inequalities

This is the second part of a free resource to help with the basic understqand...

Disclosure: This page generates income for authors based on affiliate relationships with our partners, including Amazon, Google and others.
Loading ...
Error!